How To Find Heat Released

More Tutorials Join AUS-e-TUTE Contact The states

Want chemical science games, drills, tests and more than?

You need to Bring together AUS-e-TUTE!

Heat of Solution or Enthalpy of Solution Chemistry Tutorial

Key Concepts

⚛ A solute dissolves in backlog solvent to form a solution:

solute + solvent → solution

⚛ Rut of solution, or, enthalpy of solution, is the energy released or absorbed when the solute dissolves in the solvent.

⚛ Molar heat of solution, or, molar enthalpy of solution, is the energy released or captivated per mole of solute beingness dissolved in solvent.

⚛ Heat of solution (enthalpy of solution) has the symbol^(one) ΔH_soln

⚛ Molar oestrus of solution (molar enthalpy of solution) has the units^(two) J mol^-1 or kJ mol^-one

⚛ If heat is released when the solute dissolves, temperature of solution increases, reaction is exothermic, and ΔH is negative (ΔH < 0).

solute + solvent → solution     ΔH_soln = −

solute + solvent → solution     ΔH_soln < 0

⚛ If estrus is captivated when the solute dissolves, temperature of solution decreases, reaction is endothermic, and ΔH is positive (ΔH > 0).

solute + solvent → solution     ΔH_soln = +

solute + solvent → solution     ΔH_soln > 0

⚛ Enthalpy (heat) of solution can exist determined in the laboratory by measuring the temperature change of the solvent when solute is added.

⚛ To calculate the molar enthalpy of solution (molar heat of solution) using experimental information:

Step 1: Summate the amount of energy released or captivated (q)

q = m × C_grand × ΔT

q = amount of energy released or absorbed
m = mass
C_g = specific heat capacity
ΔT = modify in temperature

Step 2: Calculate moles of solute (n)

due north = m ÷ M

northward = moles of solute
m = mass of solute
M = molar mass of solute

Pace three: Summate mount of free energy (heat) released or captivated per mole of solute (ΔH_soln)

ΔH_soln = q ÷ n

ΔH_soln = molar enthalpy (rut) of solution
q = amount of energy (heat) released or absorbed
n = moles of solute

Note: You must include the sign for ΔH_soln (either + or −)

(i) ΔH is negative if energy (oestrus) is released (exothermic).

(two) ΔH is positive if energy (heat) is captivated (endothermic).

Please practise non cake ads on this website.
No ads = no money for us = no complimentary stuff for you!

Theory Behind Determining Molar Enthalpy of Solution

The molecules or ions making upwards a solid solute exist in a highly ordered state which is referred to as a lattice.
You are probably already familiar with representations of ionic compounds in which positive ions (cations) and negative ions (anions) are bundled in a lattice held together by electrostatic forces of attraction known as ionic bonds.
The amount of disorder, or randomness, in a system is known as its entropy. A lattice is highly ordered, that is, the particles making up the lattice are in a depression state of disorder. This is referred to every bit a low entropy state⁽ⁱⁱⁱ⁾.

When this solute dissolves in a solvent, particles such as ions must be removed from the lattice and each solute particle must and then exist completely surrounded by solvent molecules.
The solute particles in the solution are in abiding motion and distributed more or less randomly throughout the solution so that the amount of disorder has increased compared to when they were part of the lattice. Solute particles in the solution are said to be in a college state of entropy than solute particles making up the lattice.

The process of dissolving a solid solute in a liquid solvent tin can therefore exist idea of every bit occurring in two steps:

If Enthalpy of Solution (estrus of solution) is Endothermic:

The magnitude of the free energy captivated to suspension up the lattice, ΔH_lat, is greater than the magnitude of the energy released when solute particles are surrounded past water solvent molecules, ΔH_hyd, so the enthalpy of solution, ΔH_soln, is positive, that is, the process is endothermic.

if |ΔH_lat| > |ΔH_hyd| and so ΔH_soln is positive

solute(southward) + water(fifty) → solution(aq) ΔHsoln = + solute(southward) + h2o(l) + ΔHsoln → solution(aq) Energy is captivated, that is, energy is a reactant. When solute is added to water, h2o temperature decreases.

ions ΔHlat ↑ | | | ΔHhyd | | | | | ↓ | solution | ↑ ΔHsoln | | salt

If Enthalpy of Solution (estrus of solution) is Exothermic:

The magnitude of the energy absorbed to break upward the lattice is less than magnitude of the energy released when solute particles are surrounded by h2o solvent molecules , then the enthalpy of solution is negative, that is, the process is exothermic.

if |ΔH_lat| < |ΔH_hyd| and then ΔH_soln is negative

solute(s) + water(l) → solution(aq) ΔHsoln = - solute(south) + h2o(l) → solution(aq) + ΔHsoln Free energy is released, that is, energy is a product. When solute is added to water, water temperature increases.

ions ΔHlat ↑ | ΔHhyd | | | | | | salt | ΔHsoln | | ↓ ↓ solution

The tabular array below lists the values of molar enthalpy of solution (molar heat of solution) for some mutual salts in water at 25°C.⁽⁴⁾

Tooth Enthalpy of Solution of Some Salts at 25°C
	Endothermic examples			Exothermic examples
Anion	solute	ΔHo soln (kJ mol-1)		solute	ΔHo soln (kJ mol-1)
chloride	NHfourCl(due south)	+xiv.78		LiCl(s)	-37.03
	NaCl(s)	+3.88
	KCl(s)	+17.22
bromide	NHivBr(s)	+xvi.78		LiBr(s)	-23.26
	KBr(due south)	+xix.87		NaBr(south)	-0.60
nitrate	NHivNOiii (s)	+25.69		LiNO3 (south)	-2.51
	AgNOiii (s)	+22.59
	NaNOthree (s)	+twenty.50
	KNOiii (s)	+34.89
hydroxide				LiOH(south)	-23.56
				NaOH(due south)	-44.51
				KOH(s)	-57.61
acetate				NH4C2HiiiOtwo (s)	-2.38
				NaC2HthreeO2 (s)	-17.32
				KC2HiiiO2 (s)	-15.33

↪ Back to top

Experiment to Determine the Tooth Oestrus of Solution (Molar Enthalpy of Solution) of a Solute

The following describes the use of a polystyrene foam (styrofoam™) cup every bit a calorimeter to determine the heat of solution of a salt (solid solute) in h2o (the solvent).⁽⁵⁾

Polystyrene cream (styrofoam™) is a good insulator, that is, it is a material that does not behave rut well.

In this experiment the polystyrene foam (styrofoam™) cup is used as an insulated vessel in which to conduct the experiment and then that either:

(i) all the energy released by the reaction is used to raise the temperature of the water in the cup and is not lost in heating the surrounding environment in the case of an exothermic reaction

(ii) the but energy being captivated past the reaction is that from the h2o in the cup and not from the surrounding surround in the case of an endothermic reaction.

Procedure:

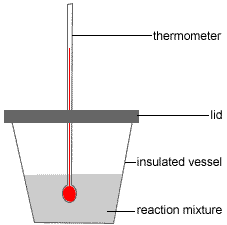
1. Step one: An accurately known quantity of water (the solvent) is placed in a well insulated vessel (eg, a polystyrene foam or styrofoam™ cup)
2. Pace two: The initial temperature of this solvent is recorded, T_i.
3. Step three: An accurately known quantity of the solid solute is added, the vessel is sealed with a chapeau and the solution stirred using the thermometer.
4. Step 4: The final temperature of the solution is recorded, T_f.

Note the final temperature will be the maximum temperature reached for an exothermic reaction or the minimum temperature reached for an endothermic reaction.

↪ Dorsum to top

Calculation of Molar Enthalpy of Solution (tooth rut of solution) ⁽⁶⁾

Step 1: Calculate the estrus released or absorbed, in joules, when the solute dissolves in the solvent:

heat released or absorbed = mass × specific heat capacity × change in temperature

q = m × c_thou × (T_concluding - T_initial )

q = m × c_g × ΔT

What is the value of mass, m? In that location are 2 ways to expect at this:
1. Method usually used by High School courses. Presume all the solute dissolves simultaneously in the solvent and so that all the heat is simultaneously captivated from, or released to, the pure solvent. k = mass of solvent in grams Sometimes the book of solvent is given rather than the mass. Convert book to mass using the density of the liquid: density = mass ÷ volume so, mass (g) = density (g mL-1) × volume (mL) density of h2o at 25°C and 101.iii kPa is usually given every bit one g mL-i So, c1000 = specific heat capacity of the solvent in J°C-1g-1 For h2o, ck = iv.18 J°C-1g-1 ΔT = Tfinal - Tinitial in °C(7) When calculated, q is in joules (J) You can convert energy in joules (J) to kilojoules (kJ) by dividing the number of joules by thou.	OR	two. Method usually used in introductory University courses. Presume the showtime molecule or ion of solute dissolves into pure solvent, simply each subsequent molecule or ion is dissolving into a mixture of dissolved solute in solvent (that is, a solution). In this case, the terminal solute molecule or ion is dissolving into a solution with a mass approximated past the mass of the solvent plus the mass of the solute. k = mass of solvent + mass of solute in grams So, cg = specific heat capacity of the solution in J°C-1m-i And, information technology is assumed that cg(solution) = cthou(solvent) in J°C-1g-1 ΔT = Tfinal - Tinitial in °C(seven) When calculated, q is in joules (J) Yous can convert energy in joules (J) to kilojoules (kJ) by dividing the number of joules past m.

Step 2: Calculate moles of solute:

moles = mass ÷ molar mass

where:

moles = amount of solute in mole

mass = mass of solute in grams

molar mass = molar mass of solute in grams per mole

Stride 3: Calculate the molar enthalpy of solution, or molar heat of solution, ΔH_soln:

ΔHsoln in J per mole of a solute is calculated:	ΔHsoln in kJ per mole of a solute is calculated:
ΔHsoln = q ÷ moles of solute (J mol-i) where q = energy released or absorbed as calculated in step 1. and moles of solute is that calculated in step 2. exothermic reactions: ΔHsoln is negative endothermic reactions: ΔHsoln is positive	ΔHsoln = q/1000 ÷ moles of solute (kJ mol-1) where q = energy released or captivated every bit calculated in stride one. and moles of solute is that calculated in footstep two. exothermic reactions: ΔHsoln is negative endothermic reactions: ΔHsoln is positive

↪ Dorsum to pinnacle

Worked Example: Sample Experimental Results and Calculations

Question:
A educatee added iv.00 1000 of NaOH(southward) to 100 g of h2o in a polystyrene foam loving cup.
The temperature of the water rose by x.0°C.
Assuming the polystyrene foam cup is well insulated and the specific heat capacity of h2o is 4.18 J°C^-1g^-ane, determine the molar enthalpy of solution of sodium hydroxide in kJ mol^-1.

Solving the Problem using the StoPGoPS model for problem solving:

STOP	STOP! State the Question.
	What is the question asking you to do? Calculate the molar heat of solution of sodium hydroxide in kJ mol-1 ΔHsoln = ? kJ mol-i
Break	Pause to Set a Game Plan
	(1) What information (data) have you been given in the question? m(NaOH) = mass NaOH(s) = 4.00 g m(H2O) = mass HiiO(l) = 100 g ΔT = temperature increase = 10.0°C cg(H2O) = specific oestrus capacity of water = 4.18 J°C-1yard-i (2) What is the relationship between what you know and what you need to discover out? oestrus released = q = one thousand × cm × ΔT moles of solute = n(NaOH) = m(NaOH) ÷ Chiliad(NaOH) ΔHsoln = q ÷ north(NaOH) Note: ΔHsoln will exist negative considering the temperature increased, that is, the procedure is exothermic.
GO	Go with the Game Program
	Method 1: (High School) Assume all solute dissolves simultaneously and instantaneously. Method 2: (University) Presume solute does non dissolve simultaneously and instantaneously. Step 1: Summate estrus released (kJ): heat released = q = grand × cg × ΔT 1000 = m(HtwoO) = 100 g ck(H2O) = 4.xviii J°C-1g-1 ΔT = 10.0°C q = 100 × 4.18 × x.0 = 4180 J q = 4180 J ÷ 1000 J/kJ = iv.18 kJ Step 2: Calculate moles of solute: moles of solute = northward(NaOH) = mass(NaOH) ÷ M(NaOH) m(NaOH) = iv.00 1000 K(NaOH) = 22.99 + 16.00 + 1.008 = 39.998 g mol-ane n(NaOH) = iv.00 ÷ 39.998 = 0.100 mol Step 3: Calculate &Delt;Hsoln ΔHsoln = q ÷ n(NaOH) ΔHsoln is negative (process is exothermic) q = 4.18 kJ due north(NaOH) = 0.100 mol ΔHsoln = -iv.eighteen ÷ 0.100 = -41.8 kJ mol-i (Note: only 3 pregnant figures are justified) Step 1: Calculate oestrus released (kJ): heat released = q = grand × cthou × ΔT m = m(H2O) + m(NaOH) = 100 + 4.00 = 104 k assume ck(solution) = cg(H2O) = iv.xviii J°C-aneone thousand-1 ΔT = ten.0°C q = 104 × 4.18 × x.0 = 4347 J q = 4347 J ÷ 1000 J/kJ = 4.35 kJ Step 2: Calculate moles of solute moles of solute = north(NaOH) = mass(NaOH) ÷ 1000(NaOH) thousand(NaOH) = 4.00 g M(NaOH) = 22.99 + sixteen.00 + 1.008 = 39.998 one thousand mol-1 n(NaOH) = 4.00 ÷ 39.998 =0.100 mol Footstep 3: Summate ΔHsoln ΔHsoln = q ÷ n(NaOH) ΔHsoln is negative (process is exothermic) q = 4.35 kJ due north(NaOH) = 0.100 mol ΔHsoln = -4.35 ÷ 0.100 = -43.five kJ mol-1 (Note: merely 3 meaning figures are justified)
PAUSE	Suspension to Ponder Plausibility
	Is your answer plausible? Work backwards: Assuming ΔHsoln ≈ -42 kJ mol-i = 42,000 J mol-i, what temperature alter is expected if four chiliad of NaOH is dissolved in 100 1000 water? ΔHsoln = q ÷ n(NaOH) rearrange: q = ΔHsoln × n(NaOH) substitute g(NaOH)/Thou(NaOH) for n(NaOH) q = ΔHsoln × m(NaOH)/M(NaOH) substitute m × cm × ΔT for q grand × cg × ΔT = ΔHsoln × m(NaOH)/Thousand(NaOH) rearrange: ΔT = [ΔHsoln × m(NaOH)/M(NaOH)]/[k × cg] substitute values: ΔT = = = ≈ [42000 × iv.00/(23 + 16 + ane)]/[100 × iv.18] [42000 × 0.1]/[418] 4200/418 ten°C Since this value for the change in temperature is the aforementioned as that given in the question, nosotros are confident our respond is correct.
STOP	STOP! State the Solution
	State your solution to the trouble. Method 1: Molar enthalpy of solution of sodium hydroxide is −41.8 kJ mol-1 ΔHsoln(NaOH) = −41.8 kJ mol-1 Method 2: Tooth enthalpy of solution of sodium hydroxide is −43.5 kJ mol-one ΔHsoln(NaOH) = −43.v kJ mol-1

↪ Back to top

Sample Question

A student added 1.92 g of KBr(southward) to 100 g of water in an insulated vessel. The temperature of the h2o fell by 0.766°C. Calculate ΔH_soln in kJ mol^-i.

↪ Back to top

---

Footnotes:

(1) If the solute and the solvent are in their standard states, you tin can too write ΔH^o _sol
Refer to Standard Enthalpy (oestrus) of Germination and Reaction

(2) You may also units of cal mol^-ane or kcal mol^-1
i calorie = 4.18 joules
1 cal = 4.18 J
For conversions between J, kJ, and cal refer to energy conversions

(3) Entropy refers to the amount of disorder, or randomness, in a organisation.
Ions locked into a crystal structure are in a low state of disorder and therefore accept low entropy.
Ions moving randomly through the solvent molecules in a solution are much more than matted, much more than random, and then they are said to be in a higher country of entropy.
Gas molecules moving randomly in the atmosphere are in an even greater country of disorder or randomness, and then they are said to accept an even higher country of entropy.
Moving towards a higher state of entropy is one of the driving forces for a chemical reaction.

(4) The values given are for solutions at space dilution which is the enthalpy change when 1 mole of solute in its standard state is dissolved in an infinite amount of h2o.

(5) Go to Calorimetry Tutorial to see an alternative method used an adiabatic solution calorimeter.

(6) On this page the calculations assume that at that place is a large excess of solvent
Note that the post-obit examples all employ the specific rut chapters of the solvent, c₁₀₀₀, not molar heat capacities, C.

(7) You lot can employ other units for temperature.
If you use Kelvin (K), and then c_m will have the same numbers but the units change to JK^-1thousand^-1. This because a change of temperature of 1K is the same every bit the change of temperature of 1°C.
If yous use fahrenheit and then you will have to apply a value for c_g that has the units J°F^-1m^-1

↪ Back to top

Source: https://www.ausetute.com.au/heatsolution.html

Posted by: hayesfacithe.blogspot.com

Share this post